In The Doppler Effect, Do Frequency, Wavelength, And/or Wave Speed Change?

Frequency modify of a moving ridge for observer relative to its source

Modify of wavelength caused past motility of the source.

An animation illustrating how the Doppler effect causes a motorcar engine or siren to sound higher in pitch when it is approaching than when it is receding. The red circles represent sound waves.

The Doppler effect or Doppler shift (or simply Doppler, when in context)^{[1] [2]} is the modify in frequency of a wave in relation to an observer who is moving relative to the wave source.^[three] It is named after the Austrian physicist Christian Doppler, who described the miracle in 1842.

A common example of Doppler shift is the change of pitch heard when a vehicle sounding a horn approaches and recedes from an observer. Compared to the emitted frequency, the received frequency is higher during the approach, identical at the instant of passing by, and lower during the recession.^[4]

The reason for the Doppler event is that when the source of the waves is moving towards the observer, each successive wave crest is emitted from a position closer to the observer than the crest of the previous wave.^{[4] [5]} Therefore, each wave takes slightly less fourth dimension to accomplish the observer than the previous wave. Hence, the fourth dimension between the arrivals of successive moving ridge crests at the observer is reduced, causing an increase in the frequency. While they are traveling, the distance between successive wave fronts is reduced, so the waves "agglomeration together". Conversely, if the source of waves is moving away from the observer, each moving ridge is emitted from a position further from the observer than the previous wave, so the arrival fourth dimension between successive waves is increased, reducing the frequency. The altitude between successive wave fronts is then increased, and so the waves "spread out".

For waves that propagate in a medium, such as sound waves, the velocity of the observer and of the source are relative to the medium in which the waves are transmitted.^[iii] The total Doppler effect may therefore result from motion of the source, motion of the observer, or movement of the medium. Each of these effects is analyzed separately. For waves which do not require a medium, such as electromagnetic waves or gravitational waves, only the relative difference in velocity betwixt the observer and the source needs to be considered. When this relative velocity is not negligible compared to the speed of light, a more complicated relativistic Doppler effect arises.

History [edit]

Experiment by Buys Ballot (1845) depicted on a wall in Utrecht (2019)

Doppler kickoff proposed this effect in 1842 in his treatise "Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels" (On the coloured lite of the binary stars and another stars of the heavens).^[6] The hypothesis was tested for sound waves past Buys Ballot in 1845.^{[p 1]} He confirmed that the sound's pitch was college than the emitted frequency when the audio source approached him, and lower than the emitted frequency when the audio source receded from him. Hippolyte Fizeau discovered independently the same phenomenon on electromagnetic waves in 1848 (in France, the effect is sometimes called "effet Doppler-Fizeau" just that name was not adopted past the rest of the world as Fizeau'south discovery was six years after Doppler's proposal).^{[p two] [7]} In Britain, John Scott Russell made an experimental study of the Doppler effect (1848).^{[p 3]}

General [edit]

In classical physics, where the speeds of source and the receiver relative to the medium are lower than the velocity of waves in the medium, the relationship between observed frequency ${\displaystyle f}$ and emitted frequency ${\displaystyle f_{\text{0}}}$ is given past:^[viii]

$${\displaystyle f=\left({\frac {c\pm v_{\text{r}}}{c\pm v_{\text{southward}}}}\right)f_{0}}$$

where

Note this human relationship predicts that the frequency will decrease if either source or receiver is moving away from the other.

Equivalently, nether the assumption that the source is either direct approaching or receding from the observer:

$${\displaystyle {\frac {f}{v_{wr}}}={\frac {f_{0}}{v_{ws}}}={\frac {i}{\lambda }}}$$

where

If the source approaches the observer at an bending (just still with a constant velocity), the observed frequency that is commencement heard is college than the object's emitted frequency. Thereafter, there is a monotonic subtract in the observed frequency equally it gets closer to the observer, through equality when it is coming from a direction perpendicular to the relative motion (and was emitted at the point of closest arroyo; but when the wave is received, the source and observer will no longer exist at their closest), and a continued monotonic subtract as it recedes from the observer. When the observer is very shut to the path of the object, the transition from high to low frequency is very sharp. When the observer is far from the path of the object, the transition from high to low frequency is gradual.

If the speeds ${\displaystyle v_{\text{s}}}$ and ${\displaystyle v_{\text{r}}\,}$ are small compared to the speed of the wave, the relationship between observed frequency ${\displaystyle f}$ and emitted frequency ${\displaystyle f_{\text{0}}}$ is approximately^[viii]

Observed frequency	Change in frequency
${\displaystyle f=\left(1+{\frac {\Delta v}{c}}\right)f_{0}}$	${\displaystyle \Delta f={\frac {\Delta v}{c}}f_{0}}$

where

Proof

Given ${\displaystyle f=\left({\frac {c+v_{\text{r}}}{c+v_{\text{s}}}}\right)f_{0}}$

we divide for ${\displaystyle c}$

$${\displaystyle f=\left({\frac {one+{\frac {v_{\text{r}}}{c}}}{1+{\frac {v_{\text{s}}}{c}}}}\right)f_{0}=\left(1+{\frac {v_{\text{r}}}{c}}\right)\left({\frac {ane}{one+{\frac {v_{\text{s}}}{c}}}}\right)f_{0}}$$

Since ${\displaystyle {\frac {v_{\text{s}}}{c}}\ll 1}$ nosotros can substitute the geometric expansion:

$${\displaystyle {\frac {1}{1+{\frac {v_{\text{due south}}}{c}}}}\approx 1-{\frac {v_{\text{s}}}{c}}}$$

• 

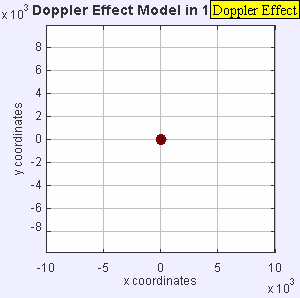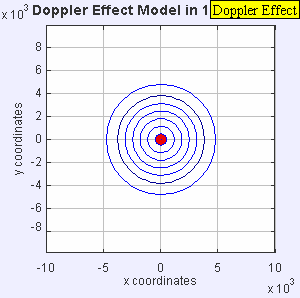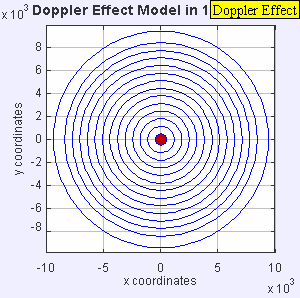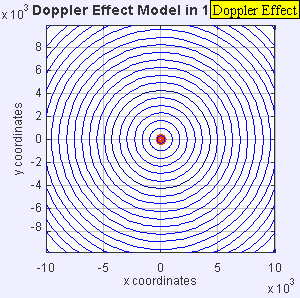
  Stationary sound source produces sound waves at a abiding frequency f , and the moving ridge-fronts propagate symmetrically away from the source at a abiding speed c. The distance between wave-fronts is the wavelength. All observers will hear the same frequency, which will be equal to the actual frequency of the source where f = f ₀ .

• 

  The same sound source is radiating sound waves at a constant frequency in the aforementioned medium. However, now the audio source is moving with a speed υ _s = 0.7 c . Since the source is moving, the centre of each new wavefront is now slightly displaced to the correct. As a result, the wave-fronts begin to agglomeration up on the correct side (in front of) and spread further autonomously on the left side (behind) of the source. An observer in front of the source will hear a college frequency f = c + 0 / c – 0.viic f ₀ = 3.33 f ₀ and an observer behind the source will hear a lower frequency f = c − 0 / c + 0.7c f ₀ = 0.59 f ₀ .

• 

  Now the source is moving at the speed of sound in the medium ( υ _{due south} = c ). The wave fronts in front of the source are now all bunched up at the aforementioned point. Equally a result, an observer in front of the source volition detect nothing until the source arrives and an observer behind the source will hear a lower frequency f = c – 0 / c + c f ₀ = 0.5 f ₀ .

• 

  The sound source has at present surpassed the speed of audio in the medium, and is traveling at 1.4 c. Since the source is moving faster than the sound waves it creates, it actually leads the advancing wavefront. The sound source will pass by a stationary observer earlier the observer hears the audio. As a result, an observer in front of the source volition notice nothing and an observer behind the source will hear a lower frequency f = c – 0 / c + 1.fourc f ₀ = 0.42 f ₀ .

Consequences [edit]

With an observer stationary relative to the medium, if a moving source is emitting waves with an actual frequency ${\displaystyle f_{0}}$ (in this case, the wavelength is changed, the transmission velocity of the wave keeps abiding; notation that the transmission velocity of the wave does non depend on the velocity of the source), then the observer detects waves with a frequency ${\displaystyle f}$ given by

$${\displaystyle f=\left({\frac {c}{c\pm v_{\text{s}}}}\right)f_{0}}$$

A similar analysis for a moving observer and a stationary source (in this case, the wavelength keeps constant, just due to the motility, the rate at which the observer receives waves and hence the manual velocity of the wave [with respect to the observer] is changed) yields the observed frequency:

$${\displaystyle f=\left({\frac {c\pm v_{\text{r}}}{c}}\right)f_{0}}$$

Assuming a stationary observer and a source moving at the speed of sound, the Doppler equation predicts a perceived momentary infinite frequency by an observer in front of a source traveling at the speed of sound. All the peaks are at the aforementioned place, then the wavelength is cypher and the frequency is infinite. This overlay of all the waves produces a shock moving ridge which for sound waves is known as a sonic smash.

When the source moves faster than the wave speed the source outruns the wave. The equation gives negative frequency values, which have no physical sense in this context (no sound at all volition be heard past the observer until the source passes past them).

Lord Rayleigh predicted the following effect in his archetype book on sound: if the observer were moving from the (stationary) source at twice the speed of sound, a musical slice previously emitted by that source would be heard in right tempo and pitch, but as if played backwards.^[ix]

Applications [edit]

Acoustic Doppler current profiler [edit]

An audio-visual Doppler current profiler (ADCP) is a hydroacoustic current meter similar to a sonar, used to measure water electric current velocities over a depth range using the Doppler effect of sound waves scattered back from particles within the water column. The term ADCP is a generic term for all audio-visual current profilers, although the abridgement originates from an instrument series introduced by RD Instruments in the 1980s. The working frequencies range of ADCPs range from 38 kHz to several Megahertz. The device used in the air for wind speed profiling using sound is known as SODAR and works with the aforementioned underlying principles.

Robotics [edit]

Dynamic real-time path planning in robotics to aid the motion of robots in a sophisticated environment with moving obstacles often take aid of Doppler upshot.^[10] Such applications are specially used for competitive robotics where the environment is constantly irresolute, such as robosoccer.

Sirens [edit]

Sirens on passing emergency vehicles.

A siren on a passing emergency vehicle will beginning out college than its stationary pitch, slide downward equally information technology passes, and go along lower than its stationary pitch as it recedes from the observer. Astronomer John Dobson explained the effect thus:

The reason the siren slides is considering it doesn't hit you lot.

In other words, if the siren approached the observer straight, the pitch would remain constant, at a higher than stationary pitch, until the vehicle striking him, then immediately spring to a new lower pitch. Because the vehicle passes past the observer, the radial velocity does not remain constant, but instead varies equally a function of the angle betwixt his line of sight and the siren'south velocity:

$${\displaystyle v_{\text{radial}}=v_{\text{s}}\cos(\theta )}$$

where ${\displaystyle \theta }$ is the angle betwixt the object'south forward velocity and the line of sight from the object to the observer.

Astronomy [edit]

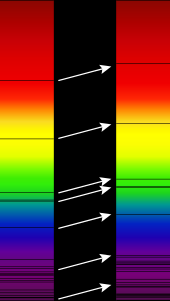
The Doppler effect for electromagnetic waves such as light is of widespread use in astronomy to measure the speed at which stars and galaxies are approaching or receding from us, resulting in and then called blueshift or redshift, respectively. This may be used to detect if an apparently unmarried star is, in reality, a close binary, to mensurate the rotational speed of stars and galaxies, or to discover exoplanets. This effect typically happens on a very small scale; there would non be a noticeable divergence in visible calorie-free to the unaided eye.^[11] The apply of the Doppler effect in astronomy depends on knowledge of precise frequencies of discrete lines in the spectra of stars.

Among the nearby stars, the largest radial velocities with respect to the Sunday are +308 km/s (BD-fifteen°4041, besides known equally LHS 52, 81.7 low-cal-years away) and −260 km/s (Woolley 9722, also known every bit Wolf 1106 and LHS 64, 78.2 light-years away). Positive radial velocity ways the star is receding from the Sun, negative that it is approaching.

Redshift is besides used to measure the expansion of space, but this is not truly a Doppler outcome.^[12] Rather, redshifting due to the expansion of infinite is known every bit cosmological redshift, which can be derived purely from the Robertson-Walker metric under the formalism of general relativity. Having said this, information technology also happens that there are detectable Doppler effects on cosmological scales, which, if incorrectly interpreted as cosmological in origin, lead to the observation of redshift-space distortions.^[xiii]

Radar [edit]

U.S. Army soldier using a radar gun, an awarding of Doppler radar, to catch speeding violators.

The Doppler outcome is used in some types of radar, to measure the velocity of detected objects. A radar beam is fired at a moving target — e.g. a motor auto, as police use radar to observe speeding motorists — as it approaches or recedes from the radar source. Each successive radar moving ridge has to travel farther to reach the car, before being reflected and re-detected near the source. As each moving ridge has to move farther, the gap between each moving ridge increases, increasing the wavelength. In some situations, the radar axle is fired at the moving car every bit information technology approaches, in which instance each successive wave travels a lesser altitude, decreasing the wavelength. In either situation, calculations from the Doppler effect accurately determine the auto's velocity. Moreover, the proximity fuze, developed during Globe State of war Ii, relies upon Doppler radar to detonate explosives at the correct time, superlative, distance, etc.^{[ citation needed ]}

Because the doppler shift affects the wave incident upon the target as well every bit the wave reflected dorsum to the radar, the change in frequency observed by a radar due to a target moving at relative velocity ${\displaystyle \Delta v}$ is twice that from the same target emitting a wave:^[14]

$${\displaystyle \Delta f={\frac {2\Delta v}{c}}f_{0}.}$$

Medical [edit]

Color flow ultrasonography (Doppler) of a carotid avenue – scanner and screen

An echocardiogram can, within certain limits, produce an accurate assessment of the direction of blood flow and the velocity of blood and cardiac tissue at whatsoever arbitrary betoken using the Doppler result. One of the limitations is that the ultrasound axle should be equally parallel to the blood catamenia as possible. Velocity measurements allow assessment of cardiac valve areas and function, abnormal communications between the left and right side of the center, leaking of blood through the valves (valvular regurgitation), and adding of the cardiac output. Contrast-enhanced ultrasound using gas-filled microbubble contrast media can be used to amend velocity or other flow-related medical measurements.^{[15] [16]}

Although "Doppler" has become synonymous with "velocity measurement" in medical imaging, in many cases information technology is not the frequency shift (Doppler shift) of the received signal that is measured, only the phase shift (when the received indicate arrives).^{[p iv]}

Velocity measurements of claret catamenia are also used in other fields of medical ultrasonography, such as obstetric ultrasonography and neurology. Velocity measurement of blood flow in arteries and veins based on Doppler effect is an effective tool for diagnosis of vascular problems like stenosis.^[17]

Period measurement [edit]

Instruments such every bit the laser Doppler velocimeter (LDV), and audio-visual Doppler velocimeter (ADV) accept been developed to measure velocities in a fluid flow. The LDV emits a calorie-free beam and the ADV emits an ultrasonic audio-visual burst, and measure the Doppler shift in wavelengths of reflections from particles moving with the flow. The actual flow is computed as a function of the water velocity and phase. This technique allows non-intrusive flow measurements, at loftier precision and loftier frequency.

Velocity profile measurement [edit]

Developed originally for velocity measurements in medical applications (claret flow), Ultrasonic Doppler Velocimetry (UDV) can measure in existent time complete velocity profile in most any liquids containing particles in suspension such as dust, gas bubbles, emulsions. Flows can be pulsating, aquiver, laminar or turbulent, stationary or transient. This technique is fully non-invasive.

Satellites [edit]

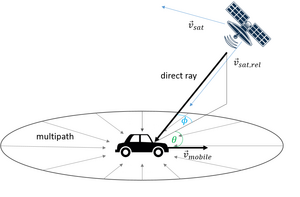
Possible Doppler shifts in dependence of the superlative angle (LEO: orbit altitude ${\displaystyle h}$ = 750 km). Fixed ground station.[eighteen]

Doppler outcome on the mobile channel. Variables: ${\displaystyle f_{c}={\frac {c}{\lambda _{\rm {c}}}}}$ is the carrier frequency, ${\displaystyle f_{\rm {D,max}}={\frac {v_{\rm {mob}}}{\lambda _{\rm {c}}}}}$ is the maximum Doppler shift due to the mobile station moving (see Doppler Spread) and ${\displaystyle f_{\rm {D,Sat}}}$ is the boosted Doppler shift due to the satellite moving.

Satellite navigation [edit]

The Doppler shift can be exploited for satellite navigation such as in Transit and DORIS.

Satellite communication [edit]

Doppler also needs to be compensated in satellite communication. Fast moving satellites can have a Doppler shift of dozens of kilohertz relative to a ground station. The speed, thus magnitude of Doppler upshot, changes due to earth curvature. Dynamic Doppler bounty, where the frequency of a signal is changed progressively during transmission, is used so the satellite receives a constant frequency signal.^[19] Later realizing that the Doppler shift had not been considered before launch of the Huygens probe of the 2005 Cassini–Huygens mission, the probe trajectory was contradistinct to approach Titan in such a way that its transmissions traveled perpendicular to its management of motion relative to Cassini, profoundly reducing the Doppler shift.^[20]

Doppler shift of the direct path tin can exist estimated past the post-obit formula:^[21]

$${\displaystyle f_{\rm {D,dir}}={\frac {v_{\rm {mob}}}{\lambda _{\rm {c}}}}\cos \phi \cos \theta }$$

where ${\displaystyle v_{\text{mob}}}$ is the velocity of the mobile station, ${\displaystyle \lambda _{\rm {c}}}$ is the wavelength of the carrier, ${\displaystyle \phi }$ is the elevation angle of the satellite and ${\displaystyle \theta }$ is the driving direction with respect to the satellite.

The additional Doppler shift due to the satellite moving can be described equally:

$${\displaystyle f_{\rm {D,saturday}}={\frac {v_{\rm {rel,sabbatum}}}{\lambda _{\rm {c}}}}}$$

where ${\displaystyle v_{\rm {rel,sat}}}$ is the relative speed of the satellite.

Audio [edit]

The Leslie speaker, most commonly associated with and predominantly used with the famous Hammond organ, takes advantage of the Doppler event by using an electric motor to rotate an acoustic horn around a loudspeaker, sending its sound in a circle. This results at the listener's ear in quickly fluctuating frequencies of a keyboard note.

Vibration measurement [edit]

A laser Doppler vibrometer (LDV) is a non-contact instrument for measuring vibration. The laser beam from the LDV is directed at the surface of interest, and the vibration amplitude and frequency are extracted from the Doppler shift of the light amplification by stimulated emission of radiation beam frequency due to the motion of the surface.

Developmental biology [edit]

During the segmentation of vertebrate embryos, waves of gene expression sweep across the presomitic mesoderm, the tissue from which the precursors of the vertebrae (somites) are formed. A new somite is formed upon arrival of a wave at the anterior end of the presomitic mesoderm. In zebrafish, information technology has been shown that the shortening of the presomitic mesoderm during segmentation leads to a Doppler-like event as the anterior terminate of the tissue moves into the waves. This effect contributes to the period of segmentation.^{[p 5]}

Inverse Doppler effect [edit]

Since 1968 scientists such as Victor Veselago have speculated nearly the possibility of an inverse Doppler effect. The size of the Doppler shift depends on the refractive index of the medium a wave is traveling through. But some materials are capable of negative refraction, which should atomic number 82 to a Doppler shift that works in a direction opposite that of a conventional Doppler shift.^[22] First experiment that detected this effect was conducted by Nigel Seddon and Trevor Bearpark in Bristol, U.k. in 2003.^{[p six]} Later inverse Doppler effect was observed in some inhomogeneous materials and predicted inside Vavilov–Cherenkov cone.^[23]

Run across too [edit]

• Bistatic Doppler shift
• Differential Doppler effect
• Doppler cooling
• Dopplergraph
• Fading
• Fizeau experiment
• Photoacoustic Doppler issue
• Rayleigh fading
• Redshift
• Laser Doppler imaging
• Relativistic Doppler upshot

Primary sources [edit]

1. ^ Buys Election (1845). "Akustische Versuche auf der Niederländischen Eisenbahn, nebst gelegentlichen Bemerkungen zur Theorie des Hrn. Prof. Doppler (in German)". Annalen der Physik und Chemie. 142 (11): 321–351. Bibcode:1845AnP...142..321B. doi:10.1002/andp.18451421102.
2. ^ Fizeau: "Acoustique et optique". Lecture, Société Philomathique de Paris, 29 December 1848. Co-ordinate to Becker(pg. 109), this was never published, but recounted by Grand. Moigno(1850): "Répertoire d'optique moderne" (in French), vol three. pp 1165–1203 and later in full by Fizeau, "Des effets du mouvement sur le ton des vibrations sonores et sur la longeur d'onde des rayons de lumière"; [Paris, 1870]. Annales de Chimie et de Physique, 19, 211–221.
3. ^ Scott Russell, John (1848). "On certain effects produced on sound by the rapid move of the observer". Report of the Eighteenth Coming together of the British Association for the Advocacy of Science. 18 (vii): 37–38. Retrieved 2008-07-08 .
4. ^ Petrescu, Florian Ion T (2015). "Improving Medical Imaging and Claret Flow Measurement by using a New Doppler Effect Relationship". American Journal of Engineering science and Applied Sciences. 8 (4): 582–588. doi:10.3844/ajeassp.2015.582.588 – via Proquest.
5. ^ Soroldoni, D.; Jörg, D. J.; Morelli, L. G.; Richmond, D. L.; Schindelin, J.; Jülicher, F.; Oates, A. C. (2014). "A Doppler Outcome in Embryonic Pattern Formation". Science. 345 (6193): 222–225. Bibcode:2014Sci...345..222S. doi:10.1126/science.1253089. PMC7611034. PMID 25013078. S2CID 206556621.
6. ^ Kozyrev, Alexander B.; van der Weide, Daniel Due west. (2005). "Explanation of the Inverse Doppler Effect Observed in Nonlinear Transmission Lines". Concrete Review Messages. 94 (xx): 203902. Bibcode:2005PhRvL..94t3902K. doi:x.1103/PhysRevLett.94.203902. PMID 16090248.

References [edit]

1. ^ U.s.. Navy Department (1969). Principles and Applications of Underwater Sound, Originally Issued equally Summary Technical Report of Division vi, NDRC, Vol. 7, 1946, Reprinted...1968. p. 194. Retrieved 2021-03-29 .
2. ^ Joseph, A. (2013). Measuring Ocean Currents: Tools, Technologies, and Information. Elsevier Science. p. 164. ISBN978-0-12-391428-half-dozen . Retrieved 2021-03-30 .
3. ^ ^{a b} Giordano, Nicholas (2009). College Physics: Reasoning and Relationships. Cengage Learning. pp. 421–424. ISBN978-0534424718.
4. ^ ^{a b} Possel, Markus (2017). "Waves, motion and frequency: the Doppler effect". Einstein Online, Vol. 5. Max Planck Institute for Gravitational Physics, Potsdam, Frg. Archived from the original on September 14, 2017. Retrieved September four, 2017.
5. ^ Henderson, Tom (2017). "The Doppler Effect – Lesson iii, Waves". Physics tutorial. The Physics Classroom. Retrieved September 4, 2017.
6. ^ Alec Eden The search for Christian Doppler, Springer-Verlag, Wien 1992. Contains a facsimile edition with an English translation.
7. ^ Becker (2011). Barbara J. Becker, Unravelling Starlight: William and Margaret Huggins and the Rise of the New Astronomy, illustrated Edition, Cambridge University Printing, 2011; ISBN 110700229X, 9781107002296.
8. ^ ^{a b} Rosen, Joe; Gothard, Lisa Quinn (2009). Encyclopedia of Concrete Science. Infobase Publishing. p. 155. ISBN978-0-8160-7011-4.
9. ^ Strutt (Lord Rayleigh), John William (1896). MacMillan & Co (ed.). The Theory of Sound. Vol. ii (2 ed.). Macmillan. p. 154.
10. ^ Agarwal, Saurabh; Gaurav, Ashish Kumar; Nirala, Mehul Kumar; Sinha, Sayan (2018). "Potential and Sampling Based RRT Star for Real-Time Dynamic Movement Planning Bookkeeping for Momentum in Cost Office". Neural Information Processing. Lecture Notes in Figurer Scientific discipline. Vol. 11307. pp. 209–221. doi:10.1007/978-three-030-04239-4_19. ISBN978-3-030-04238-seven.
11. ^ "Doppler Shift". astro.ucla.edu.
12. ^ The distinction is made clear in Harrison, Edward Robert (2000). Cosmology: The Scientific discipline of the Universe (2nd ed.). Cambridge University Printing. pp. 306ff. ISBN978-0-521-66148-5.
13. ^ An excellent review of the topic in technical detail is given here: Percival, Will; Samushia, Lado; Ross, Ashley; Shapiro, Charles; Raccanelli, Alvise (2011). "Review commodity: Redshift-infinite distortions". Philosophical Transactions of the Majestic Club. 369 (1957): 5058–67. Bibcode:2011RSPTA.369.5058P. doi:10.1098/rsta.2011.0370. PMID 22084293.
14. ^ Wolff, Dipl.-Ing. (FH) Christian. "Radar Basics". radartutorial.eu . Retrieved 14 April 2018.
15. ^ Davies, MJ; Newton, JD (2 July 2017). "Non-invasive imaging in cardiology for the generalist". British Journal of Hospital Medicine. 78 (7): 392–398. doi:10.12968/hmed.2017.78.seven.392. PMID 28692375.
16. ^ Appis, AW; Tracy, MJ; Feinstein, SB (ane June 2015). "Update on the prophylactic and efficacy of commercial ultrasound contrast agents in cardiac applications". Echo Research and Practise. 2 (two): R55–62. doi:10.1530/ERP-xv-0018. PMC4676450. PMID 26693339.
17. ^ Evans, D. H.; McDicken, W. N. (2000). Doppler Ultrasound (second ed.). New York: John Wiley and Sons. ISBN978-0-471-97001-9. ^{[ page needed ]}
18. ^ Otilia Popescuy, Jason S. Harrisz and Dimitrie C. Popescuz, Designing the Communica- tion Sub-System for Nanosatellite CubeSat Missions: Operational and Implementation Perspectives, 2016, IEEE
19. ^ Qingchong, Liu (1999), "Doppler measurement and compensation in mobile satellite communications systems", Military machine Communications Conference Proceedings / MILCOM, 1: 316–320, CiteSeerX10.1.1.674.3987, doi:10.1109/milcom.1999.822695, ISBN978-0-7803-5538-five, S2CID 12586746
20. ^ Oberg, James (October four, 2004). "Titan Calling | How a Swedish engineer saved a in one case-in-a-lifetime mission to Saturn's mysterious moon". IEEE Spectrum. (offline every bit of 2006-10-14, see Internet Archive version)
21. ^ Arndt, D. (2015). On Channel Modelling for State Mobile Satellite Reception (Doctoral dissertation).
22. ^ "Doppler shift is seen in reverse". Physics World. 10 March 2011.
23. ^ Shi, Xihang; Lin, Xiao; Kaminer, Ido; Gao, Fei; Yang, Zhaoju; Joannopoulos, John D.; Soljačić, Marin; Zhang, Baile (October 2018). "Superlight inverse Doppler result". Nature Physics. 14 (10): 1001–1005. arXiv:1805.12427. Bibcode:2018arXiv180512427S. doi:x.1038/s41567-018-0209-6. ISSN 1745-2473. S2CID 125790662.

Further reading [edit]

• Doppler, C. (1842). Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (Near the coloured light of the binary stars and another stars of the heavens). Publisher: Abhandlungen der Königl. Böhm. Gesellschaft der Wissenschaften (Five. Folge, Bd. 2, Southward. 465–482) [Proceedings of the Royal Bohemian Society of Sciences (Part 5, Vol ii)]; Prague: 1842 (Reissued 1903). Some sources mention 1843 equally year of publication because in that year the article was published in the Proceedings of the Bohemian Society of Sciences. Doppler himself referred to the publication as "Prag 1842 bei Borrosch und André", because in 1842 he had a preliminary edition printed that he distributed independently.
• "Doppler and the Doppler effect", E. Northward. da C. Andrade, Endeavour Vol. XVIII No. 69, January 1959 (published past ICI London). Historical account of Doppler's original newspaper and subsequent developments.
• David Nolte (2020). The fall and ascent of the Doppler effect. Physics Today, five. 73, pgs. 31 - 35. DOI: 10.1063/PT.3.4429
• Adrian, Eleni (24 June 1995). "Doppler Effect". NCSA. Archived from the original on 12 May 2009. Retrieved 2008-07-thirteen .

External links [edit]

• Media related to Doppler outcome at Wikimedia Commons
• Doppler Event, ScienceWorld

Source: https://en.wikipedia.org/wiki/Doppler_effect

Posted by: millercallynnusers.blogspot.com

Share this post